
Incorrect use of Excel's NPV function is a common source of spreadsheet errors. This article discusses several pitfalls and suggests ways to avoid them.
Summary of key points:
- Excel's
NPVfunction is a common source of spreadsheet errors. - Even simple spreadsheets often contain material errors.
- When using the
NPVfunction, errors that commonly occur include: referencing the wrong cells, constant jamming, inadequate documentation, inconsistent assumptions about cash flows being real/nominal and before/after tax, misinterpretation of an ambiguous model specification, and incorrect cash flow timing. - Finding and correcting errors requires inspecting every cell for errors to ensure that assumptions are consistent, functions are used correctly, good practice is followed, and the spreadsheet appropriately represents the situation being modelled.
Project evaluation using the NPV function
Many financial models use Excel's NPV function to calculate the Net Present Value of discounted cash flows. As an example, suppose we build a simple model to evaluate a project with the following specification:
- An immediate initial investment of $100m.
- Cash flows of $30m per annum throughout each of the next five years.
- A final year in which costs of $50m are incurred to complete the project (such as returning a site to greenfields condition).
- Discount rate of 7%.
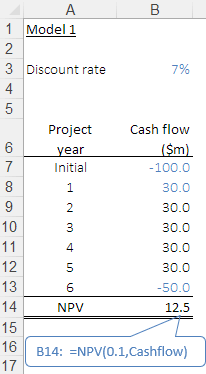
Model 1: Project evaluation NPV
Figure 1 shows Model 1, which models the project evaluation example. Note that the models described in this article are available to download.
The discount rate assumption is shown in B3. The cash flows are listed in B7:B13. The NPV of this project is calculated in B14, with a value of $12.5m. A positive NPV indicates that the project is economic, i.e. the cash flows are more than sufficient to justify the initial investment, given our discount rate. Therefore, we decide to proceed with the project.
Errors in Model 1
But hold that decision. When we inspect Model 1 we observe that there are several actual and potential errors:
- Constant jamming.
B14's formula is=NPV(0.1,Cashflow). Rather than referencing the discount rate inB3, the formula has a constant of0.1(a poor practice called "jamming"). Consequently, the NPV result is wrong since it uses an incorrect discount rate. Even if the formula contained the correct constant there would be a potential error, as a change inB3would not be reflected in the NPV. - Named range. We could assume that the named range
Cashflow, as used inB14, is correct. However, upon closer inspection we note thatCashflowis defined asB7:B12. That is, it omits the cash flow for the final year. Consequently, the NPV result is wrong. - Real or nominal cash flows. Is the discount rate real or nominal? Model 1 does not say. We must ensure that the discount rate is on the same basis as the cash flows. That is, if the cash flows grow at a rate that includes inflation, then they are nominal. If inflation has been removed from the cash flows, then they are real. Either basis could be used, depending on the model requirements. Whichever basis is used for the cash flows, the discount rate must be consistent.
- Before or after tax. Similar to the real or nominal issue described above, the cash flows may be before or after tax. Again, the discount rate must be on the same basis as the cash flows.
- Documentation. Both the discount rate and the cash flows lack documentation. They need to be documented to clearly state whether they are on a real/nominal and before/after tax basis. Other cells may also need documentation, to advise the spreadsheet's users and developers about what values are expected and how the model works.
- Cash flow timing. Excel's
NPVfunction assumes that cash flows occur at the end of each period. In our example, that assumption is incorrect, firstly because the initial investment occurs immediately, rather than being at the end of the first year, and secondly because the remaining cash flows occur throughout each year starting immediately. Therefore, the spreadsheet incorrectly models the timing of the cash flows. - Ambiguous specification. In the project specification there is some ambiguity about the timing of the costs in the final year. Do they occur at the start of the year, the end of the year, continuously throughout the year, or some other timing? Any ambiguity in the model specification must be clarified.
Model 2: Revised version that fixes the errors in Model 1
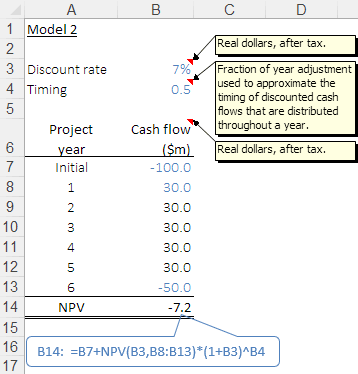
Figure 2 shows Model 2, which has been revised to fix the errors in Model 1. In this revised version, we have:
- Verified that the cash flows are on a real basis and after tax, which matches the discount rate assumption. These definitions are documented in cell comments.
- Clarified the timing of the final year costs. i.e. they are evenly spread throughout the year.
- Added an assumption in
B4, which is used to adjust the cash flow timing (as defined in its cell comment). - Changed the NPV calculation so that it refers to the discount rate assumption in
B3. - Put the initial investment outside the
NPVfunction so that it isn't discounted (i.e. it occurs immediately). - Included the final year's costs in the calculation.
- Discounted the cash flows using an
NPVfunction, with a timing adjustment to approximate cash flows that occur throughout each year rather than at the end of each year.
The NPV is now -$7.2m, almost $20m less than Model 1. Most of this change is due to including the final year costs.
Adjusting the cash flow timing also makes a material difference (increasing the NPV, by bringing forward the cash flows by half a year).
A negative NPV indicates that the project is not economic. Therefore, we decide to not proceed with the project. This decision is the opposite of that indicated by Model 1.
Conclusion
To minimise errors when using Excel's NPV function:
- Clarify any aspect of the model specification that is ambiguous.
- Ensure that you understand the implicit assumptions made by Excel's functions, such as the
NPVfunction assuming that cash flows occur at the end of each period. - Avoid putting constants in formulae.
- Include appropriate documentation so that the spreadsheet's users and developers are aware of the assumptions that are expected and how the model works.
- Be careful with the timing of discounted cash flows, ensuring that the model represents the timing correctly. It is rare that the
NPVfunction can be used without some adjustment. In many cases it may be better to discount the cash flows using formulae based on first principles, rather than using theNPVfunction, though such formulae can become complex. - Verify that named ranges reference all applicable cells.
- Inspect every cell to check for errors. This is the only robust and reliable way to ensure that the spreadsheet is correct.
Downloads
Comments
If you have any comments about this article, then please contact us.
