Authors
Elisabeth Getzner
Abstract
Spreadsheets are a popular tool often used in critical computations. Research has shown that a large percentage of professionally used spreadsheets contain errors, potentially leading to great financial losses. As a result, interest in quality assurance for spreadsheets has increased, leading to the adaptation and creation of techniques to avoid, find and repair errors in spreadsheets. One such technique is fault localization, which aids in spreadsheet debugging provided one or more cells produce an unexpected output. Fault localization uses this information to produce a set of cells that contribute to this output and may contain the fault.
In particular, spectrum-based fault localization, short SFL, ranks cells so that the highest ranked cell has the highest fault likelihood. The effectiveness of SFL is considerably impaired if two or more cells are equally likely to be faulty, forming a tie. In this thesis, we propose several improvements for SFL that either reduce the number of cells that need inspection or create additional prioritization, helping end-users to debug their spreadsheets more efficiently.
One promising improvement is Grouping, which clusters similar cells in a spreadsheet to account for the fact that many spreadsheet users copy and paste large parts of the spreadsheet. The size of the tie is reduced as grouped cells form a single unit, even though the actual number of cells in the ranking remains constant. Another possibility to improve the ranking is to reduce the input passed to SFL, resulting in a reduction of the search space. For this purpose, we propose the Blocking and Dynamic Slicing algorithms, which show moderate improvements on spreadsheets with specific structural requirements.
Tie-breaking, as opposed to input or tie reduction, focuses on increasing prioritization by breaking a set of tied cells. We propose a number of tie-breaking strategies based on position, distance and formula metrics. These strategies aim to increase the fault likelihood for suspicious cells without reducing the number of cells in the ranking. The effectiveness of tie-breaking strategies is typically dependent on the structure of the spreadsheets. We found that distance-based strategies are the most effective at prioritizing authentic faults.
We evaluate the proposed techniques using three spreadsheet corpora, two of which were created as part of this thesis. These corpora allow for a more detailed evaluation, as each offers unique structural properties. The most significant improvement over previous spreadsheet corpora is the existence of realistic testing decisions in one corpus and the existence of authentic faults in another, providing new opportunities for the evaluation of future fault localization techniques for spreadsheets.
Sample
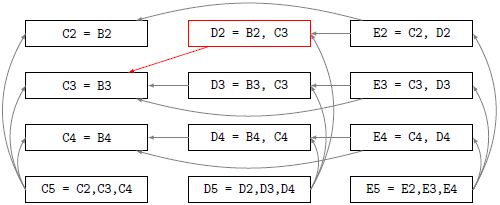
This partial program dependency graph shows the cells, their references, and the data dependency arrows. The faulty cell D2 has a red border and the faulty reference to C3 is indicated by a red arrow.
Publication
2015, Master's thesis, Graz University of Technology
Full article
Improvements for spectrum-based fault localization in spreadsheets
